To say something useful about the future of science, we need to look at the past. A long time ago, the goal of science used to be philosophical. Over time it has become more practical. We have moved from trying to answer the question of the meaning of life or what the nature of God is to the most efficient way we can produce solar cells.
However, even though the focus has shifted, we are still interested in pursuing both goals. What will be developments in science in the relatively near future?
In this article, I will have look at the development of science and see if we can predict something into the future.
Democracy
Lets first start with a quick analysis of a long term trend in scientific thinking.

Some two hundred years ago, the political system changed from aristocratic to democratic in a large part of the world. This had a profound influence on the goals of society itself.
Were these goals established by a select few people that did not need to work, after the change they were set by a much larger group of people. Even though not everybody was allowed to vote from the beginning.
The new set of society goals also changed the goals of science. Science was now to deliver results to the democratic majority of people. The democratic majority apparently mostly wanted science to improve living-standards. This then led to a greater focus on engineering/practical science and less on philosophy.



Around 1900, real-world experiments were conducted (for example by Rutherford, Curie and many others) and the underlying math was developed (i.e. by Maxwell, Einstein, Bohr and also by many others). The new tools led to a far greater understanding of our physical world around us, which led to the development of even better tools.
The scientific method changed too. To one better fitting the new goals. Trial-and-error became an important mechanism, both in practical applications and in developing new theories/models. How to filter out the errors as quick as possible became an important question (falsification: Popper).
After 1900, universal suffrage was established in most democratic societies. More, if not most, people could now vote and this probably led to changes in the goals again.
Engineering teams
As the development of our scientific tools became more and more sophisticated, the number of people needed to develop the next set of tools became greater.
Could Anthony van Leeuwenhoek make the best microscope of the time all by himself, the effort to now build the next generation of microscopes (are they even “microscopes” still?) requires a large team of people.
That is not to mention efforts like CERN, the ITER Tokamak, space travel or DNA sequencing. They all require large groups of people cooperating.
Another example would be the development of computers: The computer was never invented by a single person. Instead, it was an engineering development to which very many people contributed. The first computers have helped propel scientific knowledge even higher and then to the development of better computers etc. Science without computers nowadays is nearly impossible.
So is there still a role for individual genius nowadays? Will there be another Einstein in our lifetimes?
As each generation needs their own heroes, there probably will be. But these new heroes will in all likelihood not be “real” ones: The development of the next generation of scientific tools will most likely be more of a team effort.
Mathematics
At this point, I would like to delve into some specific scientific issues. Which bits of the scientific arena are stuck? Where could we expect further development? Starting with mathematics in general.
Looking into the rear-view mirror, one could say that mathematics as we use it today was probably somewhat ‘invented’ by Rene Descartes. The biggest successes were maybe scored by Newton, Maxwell and Einstein. They all developed mathematics further in a way that actually described observed phenomena, had a practical application and thus helped engineering forward in big leaps.
The success of these mathematicians (fame!) may have led to an overestimation of what mathematics can do. A lot of people, motivated by the fame of these past successes, tried to explain other unexplained observations using mathematics. In particular the observations that led to quantum mechanics.
For example: even though a lot of different explanations are possible to explain the double-split experiment, a mathematical explanation was sought and found. Unfortunately, it became so convoluted as to become suspicious (Occam’s razor). Almost too esoteric and a possible candidate to be replaced with something more worldly, in my opinion.
In the end, we made the mathematics fit, but had no real-world model anymore of what is actually going on.
The Brownian motion
Interesting in this context is Einstein’s paper regarding the Brownian motion.
When small bits of a shining material are floating in a glass of water and a light is shone on them, the reflections on the wall (it looks like a disco-ball!) will move. You might think that is because the water is just poured and little currents are still flowing inside the glass. However, and this is the key observation, even if you leave the glass for a long time, the movement of the light-reflections does not slow down! That is strange.
A number of theories can be draw up to explain the observation. Easily. Maybe there is an electrical current flowing through the bits of metal that attract and/or repel each other (there isn’t).
It was Einstein, though, who explained the movements by assuming water molecules exist, that move and bump around, also against the bits of mirror in the water. He showed that if you assume that and then calculate the statistics, you can explain the movements of the little mirrors and the light-spots on the wall.

In effect, he made the assumption of the existence of molecules (further unobservable at the time), believably true. He did this using mathematics.
In doing so, he also added a whole level of smaller scale, a new world (atoms!) to the known scientific world. These atoms were too small to observe and smaller than the scale science had been operating on thus far.
Scale
Einstein made a level of smaller scale than the known ones more believable at the time. A littler world.
The immediate question arising is, off-course, what the world would look like at the next smaller scale! Is there one or have we discovered the smallest (fundamental) scale of things? (no)
About one hundred years ago, a lot of new physical observations were made. Mainly because of the new tools that were becoming available. Radiation is a good example, where many observations were made by Rutherford and Curie. This led to the discovery of the atomic scale.
Where atoms (probably) had existed before, they were only discovered by scientists then. Nowadays, we do believe there is a next smaller level of scale in the quantum world.
We cannot, at present, directly observe this smaller level of scale. But we can make some statistical observations. Similar to the statistics of the Brownian motion: we can observe a large number of photons in certain experiments and draw conclusions about the next smaller level from that. Or we can collide a lot of elementary particles (never directly observed), follow the trajectories they make and derive statistics from that (CERN). Gives us enough confidence to declare that a Higgs-boson must exist. Statistics statistics…
But does a smaller level of scale exist even beyond that? Might there be, for example, little rocket-men flying around in tiny little space-ships, pushing Higgs-bosons in the right directions? We do not know. Might there be an aether that supports all kinds of waves of some sort? Might this actually be 7-dimensional?
The smallest thing that we ‘know’ to exist is probably the Planck-distance. It is a long story, but it appears there is a minimum distance, a discrete distance, that objects can move in. No object can move a smaller distances than that. This is called the Planck-distance and it is very, very, very small: about 1.6×10−35 m
To put that distance into perspective: the width of a water molecule (H2O) is estimated to be about 2.75×10-10 — That is MUCH bigger!
So, if a tiny little rocket-man was, say 10-30 m, there could be 1020 (or 100000000000000000000) of them fitted within a single water molecule.
It seems there could be plenty of levels-of-scale between the atomic-scale and the smallest scale to be discovered yet!
Consider this picture as an example of some scale orders of magnitude:
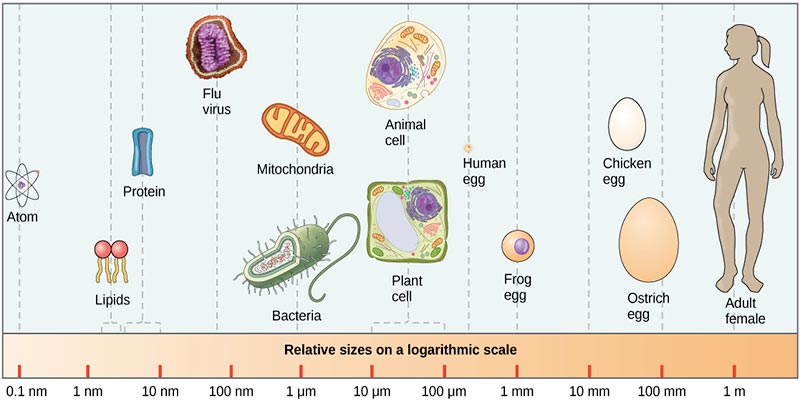
In the picture above, I would probably determine three levels of scale. On the left is the atomic scale, middle is the live-nano meter-DNA-peptide scale and right the biological (human) scale. The picture, from left to right is about 1010 in order-of-magnitude scale difference and contains 3 different scales.
So, very heuristically, we could take 105 as one order of magnitude. Doing that and continuing smaller (there is no reason except imagination to do so), there would be 5 orders of magnitude between the atomic scale and the Planck-scale. 5 entire worlds with their own rules to be discovered…. LOL!
The next level of small
The development of new tools is now a huge team effort. To discover a smaller world than the currently known one (or a bigger universe than the currently known one) we need a next generation of scientific tools. These new tools will tell us more about the nature of reality and may also propel engineering and our quality of life forward.
These next generation of tools will also probably be hugely expensive and require large teams of people to build. The discoveries will be harder to find.
Live itself
We have not even out-explored the currently known levels of scale. The DNA/peptide/virus scale is largely unexplored, for example.
The exploration of the world around 1700 was easy: map what you know, look at a world map, get a ship together (team effort) and sail towards an unmapped area.
The live/DNA scale is where a lot of exploration is to be done now. Same recipe: map what we know and fill in the gaps. It will bring a lot of benefits, obviously.
Engineering will progress!